陈昱安课题组提出在二维系统中提取广义泡利稳定码拓扑序的算法
2024-08-14
北京大学物理学院量子材料科学中心陈昱安助理教授与合作者在量子计算领域取得重要进展。研究团队提出了一种算法,可以从二维广义泡利稳定子码中提取拓扑数据。2024年8月8日,相关成果以“在二维系统中提取广义泡利稳定子码的拓扑序”(Extracting topological orders of generalized Pauli stabilizer codes in two dimensions)为题,在线发表于《物理学评论X 量子》(PRX Quantum)上。
在迅速发展的量子计算领域,量子码的鲁棒性和多功能性对于构建实用且抗干扰的系统至关重要。本文介绍了一种新颖的算法,该算法显著扩展了我们从二维量子系统的广义泡利稳定子码中提取和分析拓扑序的能力。这一进展不仅加深了我们的理论理解,也提升了量子纠错的实际应用,这对构建可靠的量子计算机至关重要。
以往对量子码的研究通常集中在素数维度的量子比特(qudit),即其限制在有限的环面码(toric code)上。我们新引入的算法突破了这个限制,成功应用于非素数维度的量子比特上,如图1(左)所示的六半子稳定子码(six-semion stabilizer code)。这种扩展的适用性使研究人员能够探索更广泛的量子系统,发现以前难以观察到的拓扑序。并且我们可以通过算法高效地设计和验证新的量子纠错码,如图1(右)所示的自对偶CSS量子码。
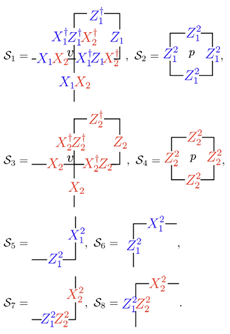
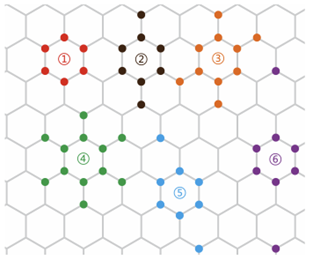
图1:(左)六半子稳定子码(Six-semion stabilizer code)。在四边形晶格上,每条边上有两个Z4的量子比特。(右)六个自对偶CSS量子码的例子。在六边形晶格上,每个顶点上有一个Z2的量子比特。例如:第一个是色码(color code),它由图中所示模样的全都是X和全都是Z的两个稳定子构成。
该算法的核心在于将拓扑序的识别转换为可管理的计算任务,通过高斯消元、Smith标准形等数学工具,算法可以确定所有的任意子(anyon)及其弦算符(string operator),然后计算它们的融合规则(fusion rule)、拓扑自旋(topological spin)和编织统计(braiding statistic),从而全面解析广义泡利稳定子码的拓扑属性,其流程如图2所示。
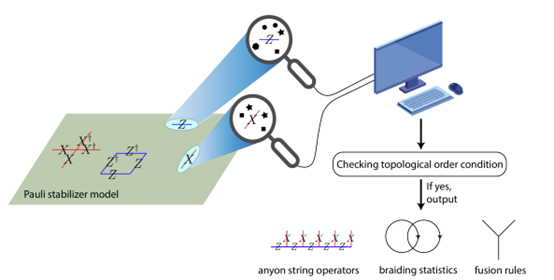
图2:算法的流程。我们想确定给定的泡利稳定子模型是否呈现拓扑序,并给出任意子弦算符、编织统计和融合规则。首先,记录单个泡利算符的对于不同稳定子违反的情况。接下来,使用我们算法来检查稳定子码是否满足拓扑序条件。如果满足,该算法可以获得给定模型的拓扑数据。
该研究不仅在理论上有重要突破,还在实际应用上展示了广泛的前景。随着量子计算技术的进步,理解和利用量子系统的拓扑性质对于发展更强大的量子计算平台至关重要。此项研究工作展示了一种有效的拓扑数据提取方法,在未来的量子技术应用中发挥关键作用。
北京大学物理学院量子材料科学中心2024级博士生梁子健和马里兰大学的博士生许逸葭为论文的共同第一作者,陈昱安为通讯作者,其他合作者包括马里兰大学的博士生Joseph T. Iosue。
文章链接:https://journals.aps.org/prxquantum/abstract/10.1103/PRXQuantum.5.030328