Discovery of Log-Periodic Quantum Oscillation: A New Chapter of Quantum Oscillations
Scientists have discovered log-periodic quantum oscillations in a solid-state system for the first time. This discovery represents the third known class of quantum oscillations after a nearly 90 year history of quantum oscillationmeasurements.
Background: quantum oscillations
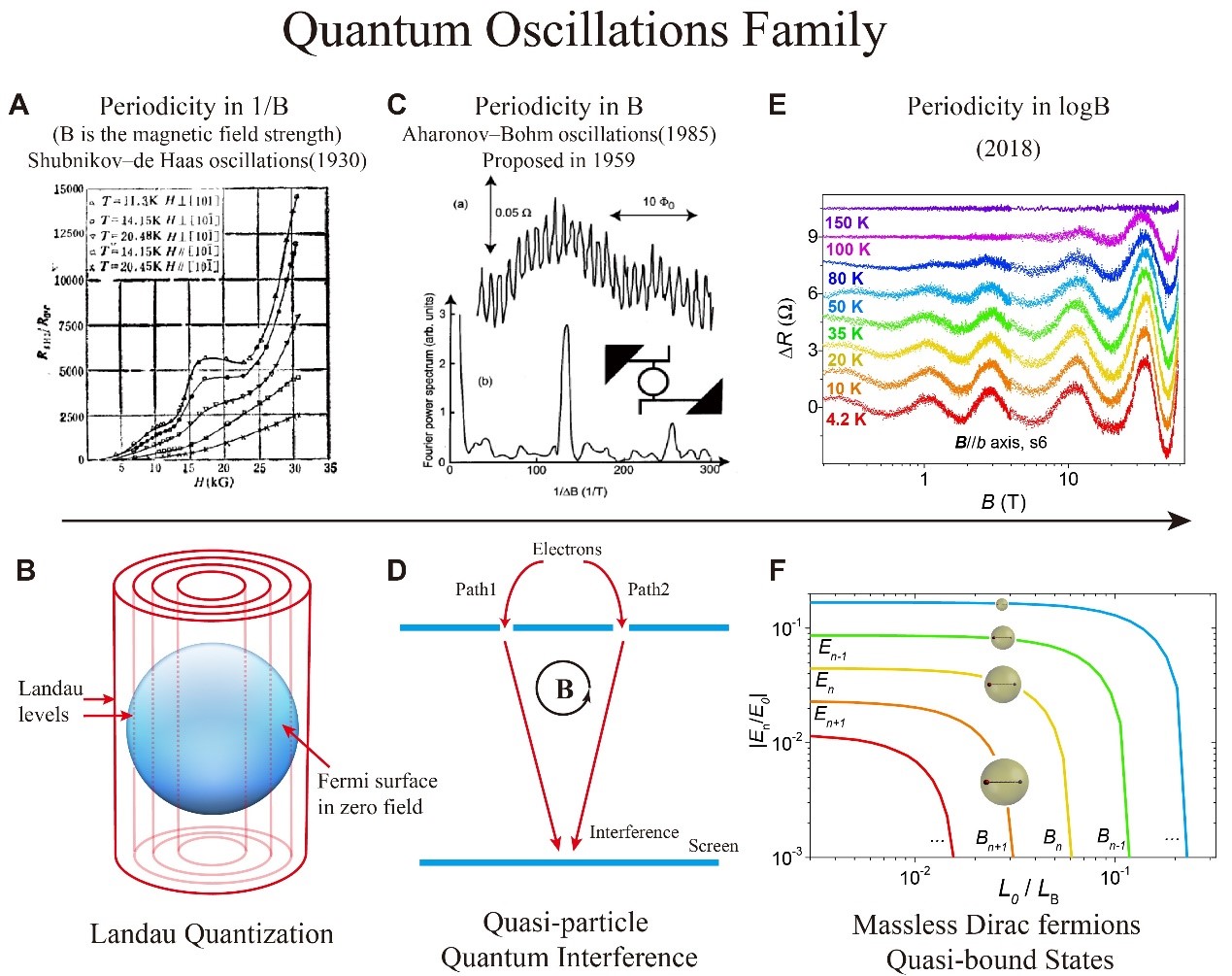
In 1930, Lev Shubnikov and W. J. de Haas first observed that the resistance of a single crystal of bismuth changes periodically with the reciprocal of the magnetic field (1/B). This phenomenon is now known as Shubnikov-de Haas (SdH) magnetoresistance oscillations. Since then, the quantum oscillation experiments have gradually evolved into a powerful experimental technique to reveal novel physical phenomena in solid state systems. Over the past 90 years, researchers have observed quantum oscillations in diverse materials, including metals, metallic compounds, semimetals, semiconductors (and even insulators), as well as in artificial mesoscopic microstructures. To date, all known quantum oscillations can be classified into two classes: the first type is quantum oscillations with a periodicity in 1/B. A typical example is the SdH oscillations in magnetoresistance arising from Landau quantization, which has become an important experimental method to map out the Fermi surface and related physical properties of materials (See Figure 1 (A and B)). The second type is periodic in B, originating from the quasi-particle quantum interference in mesoscopic systems, such as the Aharonov–Bohm (AB) and Altshuler-Aronov-Spivak (AAS) oscillations in ring or cylinder structures in magnetoresistance (See Figure 1 (C and D)). Historically, each type of quantum oscillation reflects an important underlying physical mechanism and corresponds to new physical laws.
Discovery of Log-Periodic Quantum Oscillation
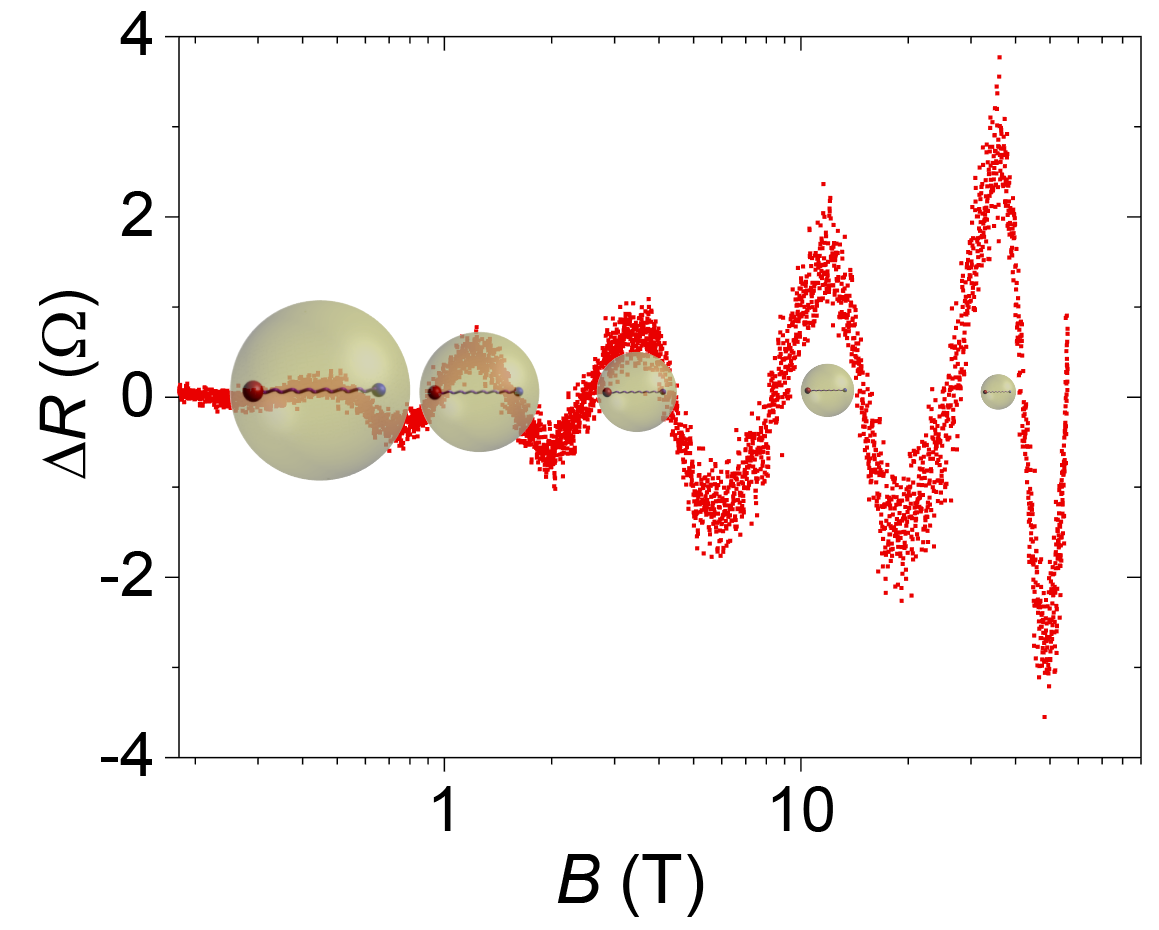
Recently, a research collaboration led by Prof. Jian Wang and Prof. Xincheng Xie at Peking University has discovered a new log-periodic quantum oscillation in high-quality single-crystal ZrTe5, a three-dimensional layered topological material. Under a strong magnetic field, transport carriers of the topological material enter the lowest Landau level, the so-called quantum limit. Beyond the quantum limit of ZrTe5, the research team discovered log-periodic oscillations involving up to five oscillating cycles (5 peaks and 5 dips) in magnetoresistance. This novel discovery is further confirmed by the magnetotransport results from different samples and different facilities with the maximum magnetic field up to 58 Tesla (See Figure 1 (E)).
The observed oscillations with the log-periodicity are different from all previously known quantum oscillations. Detailed analyses show that the log-periodic oscillations cannot be attributed to conventional type of quantum oscillations, even considering Zeeman splitting in the SdH mechanism. This indicates that the novel log-periodic quantum oscillation is a new member of the quantum oscillation family. Furthermore, the observed oscillations cannot be explained by previously known mechanisms beyond the quantum limit, such as the fractional quantum Hall states, Wigner crystal or density wave transition. This discovery potentially points to a new quantum state beyond the quantum limit.
Log-periodic quantum oscillation: discrete scale invariance in a quantum material
Further analyses reveal that the novel log-periodicity of the oscillating structures in the magnetoresistance demonstrates the existence of discrete scale invariance (DSI). A system with (continuous) scale invariance means that it can reproduce itself on different temporal or spatial scales. DSI is a partial breaking of continuous scale invariance, and subsequent observables of the system obey the scale invariance only for a geometrical set of characteristic length scales. The signature of DSI, log-periodicity, exists in animals, growth processes, financial crisis, earthquakes, turbulence, and so on. In a classical physical system, the DSI exists in the fractal structure induced by non-linear equations. Figure 2A shows a woodcut “Circle Limit III” by M. C. Escher, which represents a famous fractal structure ——the Poincaré disk model. In quantum systems, the best-known system with DSI is the Efimov trimer bound state, which has been observed in cold atom experiments and has inspired a growing research interest in related fields.
Log-periodic quantum oscillation: relativistic quantum quasi-bound states of supercritical atomic collapse
For solid-state systems, Dirac semimetals provide a promising platform to search for this rare and important phenomenon in quantum physics. On the other hand, relativistic quantum mechanics predicts that when the charge of a superheavy atomic nucleus Z exceeds a certain value satisfying Zα>1 (here α is the fine structure constant and α~1/137), the resulting strong Coulomb attraction causes an unusual atomic collapse state. This supercritical collapse state is a fundamental problem of nuclear physics, chosen by Science magazine as one of the 125 important scientific questions for humanity. However, this important theoretical prediction has not been directly confirmed in experiments. In Dirac materials, the quasi-particles (transport carriers) obey the relativistic equation, and the value of effective fine-structure constant in Dirac materials is much larger than the value in vacuum. Consequently, the supercritical collapse condition can be easily attained in Dirac materials, which provides a potential platform to study this peculiar phenomenon. In the Dirac material ZrTe5, the light holes obey the massless Dirac equation and their Fermi velocity is 450 km/s, much smaller than the speed of light in vacuum. Thus, the effective fine-structure constant of the system α>1, guaranteeing the supercritical collapse condition and giving rise to quasi-bound states with a finite lifetime. Meanwhile, these two-body quasi-bound states obey the DSI. These quasi-bound states in the supercritical regime can be considered as artificial atoms. Without magnetic field, these quasi-bound states obey DSI in both energy spectrum and radius. Under magnetic field, the energy of quasi-bound states approaches the Fermi surface at the corresponding magnetic field value obeying the geometric progression (See Figure 1F). The elastic scattering between the mobile carriers and the quasi-bound states around the Fermi energy strongly influences the transport properties, which gives rise to a log-periodic correction to the magnetoresistance. Furthermore, the SdH oscillations no longer survive beyond the quantum limit, and thus the signal of the log-periodic quantum oscillations can be clarified. Therefore, the discovery of the exotic log B periodic oscillations could virtually represent DSI for the quasi-particles in topological materials. Figure 2B shows the Russian doll analogy of the DSI in a Dirac system. Moreover, the investigation of these peculiar quasi-bound states in Dirac materials can broaden our understanding of supercritical atomic collapse.
Log-periodic quantum oscillation: a universal behavior in Dirac or topological materials
Based on this work, the research collaboration led by Prof. Jian Wang has found that the novel log-periodic oscillations and DSI features are potentially universal in topological materials with Coulomb attraction (arXiv:1810.03109). Hopefully, topological materials will become an interdisciplinary research platform to bridge the gap between the DSI and supercritical atomic collapse phenomenon. Thus, the discovery of the log-periodic oscillations provides a new experimental tool for exploring novel relativistic quantum phenomenon beyond condensed matter physics.
Publication and Acknowledgements
The paper was published in Science Advances on November 2, 2018, Eastern Time. (Science Advances, 4,eaau5096 (2018).DOI: 10.1126/sciadv.aau5096) (Link: http://advances.sciencemag.org/content/4/11/eaau5096.)
Dr. Huichao Wang at Peking University and Prof. Haiwen Liu at Beijing Normal University contributed equally to this work. Prof. Jian Wang, Prof. X. C. Xie at Peking University are corresponding authors of this paper. Prof. Junfeng Wang and Prof. Liang Li at Wuhan National High Magnetic Field Center, Prof. Jiaqiang Yan and Prof. David Mandrus at Oak Ridge National Laboratory, Prof. Yong Wang at Zhejiang University and Prof. Jiyan Dai at The Hong Kong Polytechnic University collaborated on this project. We gratefully thank Prof. Robert Joynt at University of Wisconsin, Prof. Ziqiang Wang at Boston College, and Prof. Hui Zhai at Tsinghua University for helpful suggestions to the theoretical analysis.
This work was supported by the National Basic Research Program of China, the National Natural Science Foundation of China, the Research Fund for the Doctoral Program of Higher Education of China, the Open Project Program of the Pulsed High Magnetic Field Facility, the Key Research Program of the Chinese Academy of Sciences, the US Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division, the Gordon and Betty Moore Foundation’s EPiQS Initiative and the Postdoctoral Fellowships Scheme of the Hong Kong Polytechnic etc.
Fig. 1. Quantum Oscillations Family. (A and B) Quantum oscillations with a periodicity in 1/B. A typical example is the Shubnikov-de Haas (SdH) oscillations arising from the Landau quantization in magnetoresistance. (A) From [1]. (C and D) Quantum oscillations with a periodicity in B, such as the Aharonov-Bohm (AB) and Altshuler-Aronov-Spivak (AAS) oscillations arising from the quasi-particle quantum interference in magnetoresistance. (C) From [2]. (E and F) Quantum oscillations with a periodicity in logB. Massless Dirac fermions with supercritical Coulomb attraction can give rise to the two-body quasi-bound states with discrete scale invariance. The quasi-bound states approach the Fermi energy under the magnetic field one after the other, and induce the log-periodic quantum oscillations in magnetoresistance.
[1] L. Schubnikow and W. J. De Haas, Nature (London) 126,500 (1930).
[2] R. A. Webb, S. Washburn, C. Umbach, and R. A. Laibowitz, Phys. Rev. Lett. 54, 2696 (1985). Theoretically proposed in 1959 by Aharonov and Bohm.
Fig. 2. Systems with discrete scale invariance (DSI). (A) “Circle Limit III” by M. C. Escher, which represents Poincaré disk model, a famous fractal structure. (From [3]) (B) Two-body quasi-bound states of massless Dirac fermions with supercritical Coulomb attraction. Inset is the Russian doll analogy of the discrete scale invariance in a Dirac system, the log-periodic quantum oscillations.
[3] M. C. Escher, Circle Limit III, (1959).